y=a(x-h)^2+k。
2次函数顶点式是什么。1
二次函数顶点式解析式是:y=a(x-h)^2+k。
1、开口方向:当a0时,开口向上;当a0时,开口向下。
2、顶点:(h,k)。
3、对称轴:直线x=h。
4、最值:当a0时,y有最小值k;当a0时,y有最大值k。
5、当a0时,在对称轴的左半侧,y随x的增大而减小;在对称轴的右半侧,y随x的增大而增大。
当a0时,在对称轴的左半侧,y随x的增大而增大;在对称轴的右半侧,y随x的增的而减小。
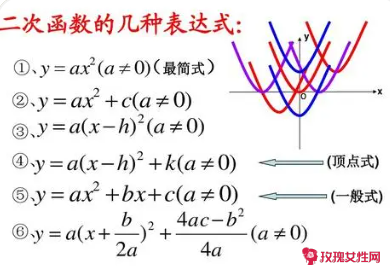
二次函数其表达式有三种:
1、一般式
y=ax^2+bx+c(a≠0,a、b、c为常数)。
2、顶点式:
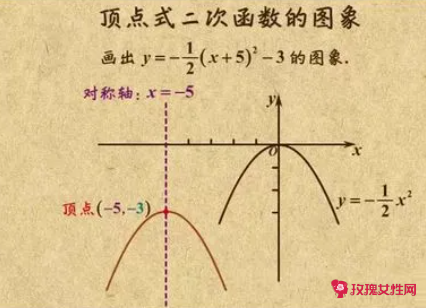
y=a(x-h)^2+k(a≠0,a、h、k为常数),顶点坐标为(h,k)对称轴为x=h,顶点的位置特征和图像的开口方向与函数y=ax^2的图像相同,有时题目会指出让你用配方法把一般式化成顶点式。
3、交点式
y=a(x-x1)(x-x2)(a≠0)[仅限于与x轴即y=0有交点A(x1,0)和B(x2,0)的抛物线,即b2-4ac≥0]。
二次函数顶点式怎么求
是二次函数y=ax^2+bx+c(a≠0)的顶点纵坐标公式
坐标(-2a/b,4ac-b2/4a)
二次函数表达式为y=ax2+bx+c(且a≠0),它的定义是一个二次多项式(或单项式)。
如果令y值等于零,则可得一个二次方程。该方程的解称为方程的根或函数的零点。
二次项系数a决定抛物线的.开口方向和大小。当a0时,抛物线开口向上;当a0时,抛物线开口向下。|a|越大,则抛物线的开口越小;|a|越小,则抛物线的开口越大。
一次项系数b和二次项系数a共同决定对称轴的位置。当a与b同号时(即ab0),对称轴在y轴左侧;当a与b异号时(即ab0),对称轴在y轴右侧。(可巧记为:左同右异)
扩展资料:
y=a(x-h)2+k(a≠0,a、h、k为常数),顶点坐标为(h,k) ,对称轴为直线x=h,顶点的位置特征和图像的开口方向与函数y=ax2的图像相同,当x=h时,y最大(小)值=k.有时题目会指出让你用配方法把一般式化成顶点式。
例:已知二次函数y的顶点(1,2)和另一任意点(3,10),求y的解析式。
解:设y=a(x-1)2+2,把(3,10)代入上式,解得y=2(x-1)2+2。
注意:与点在平面直角坐标系中的平移不同,二次函数平移后的顶点式中,h0时,h越大,图像的对称轴离y轴越远,且在x轴正方向上,不能因h前是负号就简单地认为是向左平移。
2次函数顶点式是什么。2
交点式二次函数表达式是什么
交点式二次函数表达式为:y=a(X-x1)(X-x2) [这个仅限于与x轴有交点A(x1,0)和B(x2,0)的抛物线]。交点式二次函数通常可用来解决与二次函数的图象和x轴交点坐标有关联的问题。

拓展
交点式的推导是什么
交点式的`推导是:
假设y=ax2+bx+c此函数与x轴有两交点,也就是说ax2+bx+c=0有两根,分别是x1,x2,
a(x2+bx/a+c/a)=0根据韦达定理可知a[x2-(x1+x2)x+x1*x2]=0
即十字交叉相乘:
1x -x1
1x -x2
a(x-x1)(x-x2) 就是这样推出来的。
解决二次函数,还有一般式和顶点式两种
一般式为:y=ax2+bx+c
顶点式为:y=a(x-h)2+k
交点式为:y=a(x-x1)(x-x2) [仅限于与x轴有交点A(x1,0)和 B(x2,0)的抛物线]
一般情况下,如果a、b、c是常数(其中a≠0),那么y就叫做x的二次函数。
2次函数顶点式是什么。3
一、标准差函数的原理
标准差在统计学中是一个很重要的概念,用于衡量一组数据的离散程度,反映了数据分布的散布程度和偏离程度。 在Excel中,标准差的计算公式为STDDEV.S,用公式表示为:
STDDEV.S([number1],[number2],[number3],...)
其中[number1],[number2],[number3]… 表示数据值,数据之间必须用逗号分隔。
二、标准差函数的特点
1、标准差函数的结果为实数值,表示一组数据的离散程度。
2、标准差函数适用于不同类型的数据,如财务、科学、生物、社会等多个领域。
3、标准差函数可以针对一组数据的样本进行计算,也可以针对整个数据集进行计算。
三、标准差函数的使用方法
在Excel中,使用标准差函数很简单。只需要在括号中输入数据值,用逗号分隔即可。接下来我们将逐步介绍如何使用标准差函数。
1、标准差函数的使用方法
打开Excel,从数据菜单栏中选择统计函数,然后选择标准差(STDDEV.S)函数。此时弹出一个对话框,让你输入单元格的范围,你要求标准差。选择范围后,单击确定即可计算标准差。
2、使用标准差函数进行简单的数据分析
在Excel中,可以使用标准差函数来进行一些简单的数据分析。例如,考虑以下数据集:
1,2,3,4,5
要求标准差,可以输入以下公式:
=STDDEV.S(1, 2, 3, 4, 5)
然后按回车键即可计算标准差。Excel会将结果呈现在单元格中,如下所示:
1.58
这意味着,上述数据集的标准差为1.58。
3、使用标准偏差函数进行高级数据分析
在Excel中,可以使用标准偏差函数来进行高级数据分析。标准偏差是标准差的平方根,用于衡量一组数据的变化程度。它可以提供比标准差更具描述性的信息。
例如,考虑以下数据集:
1,2,3,4,5
要求标准偏差,可以输入以下公式:
=STDEV.S(1,2,3,4,5)
然后按回车键即可计算标准偏差。 Excel会将结果呈现在单元格中,如下所示:
1.41
这意味着,上述数据集的'标准偏差为1.41。
四、标准差函数的注意事项
1、在使用标准差函数时,要注意数据之间的逗号分隔。
2、通过计算标准差函数,可以快速确定数据的离散程度,而不必通过手工计算每个数字。
3、在Excel中可以使用标准偏差函数来进行高级数据分析。
使用标准差函数是Excel中非常重要的函数之一,它可以衡量数据的波动范围。在统计多个数字的标准差时,使用Excel可以更加方便、准确和快速。同时,配合其他的Excel函数,例如,图表、显示、筛选等等可以进行更加高效的数据分析。建议大家多看一下Excel函数的使用,可以更加熟练地使用Excel完成各种数据处理和分析任务。
【2次函数顶点式是什么。】相关文章:
excel函数求和公式08-10
分居式的婚姻03-04
春分是什么意思代表的是什么06-12
see的过去式08-09
think的过去式08-05
甘油的化学式07-15
usd是什么08-05
情商是什么04-03
荷尔蒙是什么07-28